Introductory example
In Financial mathematics we start with compound interest calculation, and I try to make the math as relatable as possible and showing students its relevance in everyday life. The introduction example as follows:
The share market is swaying all the time. Here is an example. You have invested 100000 € in an ethic fund. It’s not important that it is an ethic fund, but it makes it more suggestive. Think about it: An ethic fund! Why on earth did I put my money in that? Well, this fund moves all the time. Day 1 it increases with 1 %. Day 2 it decreases with 1 %. Day 3 it increases again with 1 %. Etc.
a) What will the value of the fund be after 1000 days?
- What a question! Of course, 100000 €
- One percent more than 100000 € (101000 €).
- One percent less than 100000 € (99000 €).
- More than that.
- Less than that.
At first, think about the right answer without Excel.
Sometimes there are some bright students that immediately realize the connection between the task and percentage calculation. But quite often, I will get a lot of wrong answers. This example is brilliant, containing both percentage comprehension and compound interest calculation. This highlights how practical applications can make mathematical concepts click for students.
In part b), we calculate the correct answer and the change in percentage with Excel.
Compound interest
Further on in the course we calculate with the power of interest-on interest thinking. The two components affecting your investment are time and rate. Compound interest is a powerful financial concept where the interest earned on an initial amount (the principal) also earns interest over time. Unlike simple interest, which i calculated only on the principal amount, compound interest grows exponentially because it includes interest from previous periods. The following examples show the importance of the components time and rate.
Example1.
Draw a line chart of a 1000-euro investment in 20 years with interest rates 3,6,9,12 and 15 %.
Answer:

Example2.
Draw a bar chart of a 1000-euro investment at interest rate 10% for 5, 10,15, 20 and 25 years.
Answer:

Obviously, it is important to keep the interest rate at as a high rate as possible (exercise 1) and to save the money for as long time as possible (exercise 2). In both exercises the change is exponential, not linear. This distinction is crucial, especially in fields like finance.
Example3.
Draw a line chart of a 1000-euro investment for 10 years with the following annual changes:
| Year | Serie1 | Serie2 | Serie3 | Serie4 | Serie5 | Serie6 | Serie7 |
| 1 | 10 % | 20 % | 1 % | 14 % | -3 % | -16 % | -8 % |
| 2 | 10 % | 0 % | 13 % | 11 % | 22 % | 43 % | -29 % |
| 3 | 10 % | 6 % | 14 % | 8 % | -4 % | 31 % | -27 % |
| 4 | 10 % | -11 % | -3 % | 6 % | 14 % | -15 % | 29 % |
| 5 | 10 % | 23 % | 25 % | 15 % | -4 % | 11 % | 12 % |
| 6 | 10 % | -3 % | -15 % | 4 % | 23 % | 7 % | 31 % |
| 7 | 10 % | 18 % | 7 % | 26 % | 10 % | -25 % | 18 % |
| 8 | 10 % | 24 % | 28 % | -19 % | 21 % | 22 % | 31 % |
| 9 | 10 % | -2 % | 20 % | 17 % | 6 % | 29 % | 27 % |
| 10 | 10 % | 25 % | 10 % | 18 % | 15 % | 13 % | 16 % |
| Total | 100 % | 100 % | 100 % | 100 % | 100 % | 100 % | 100 % |
Which option is the best one?
Answer:
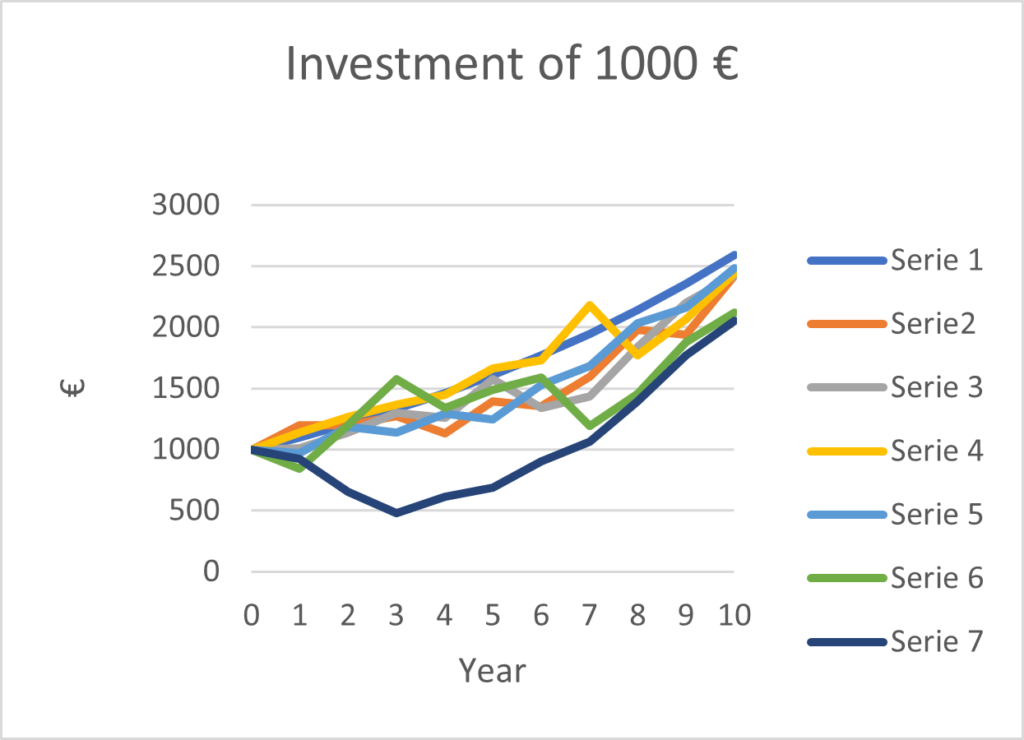
When you are saving money, it is almost impossible to obtain the same return or investment rate each year. But a constant return must be something worth achieving.
Albert Einstein and compound interest
Albert Einstein, one of the greatest minds of the 20th century, is best known for his work in theoretical physics, particularly his theory of relativity. However, his insights extended far beyond thefield of physics, touching on profound truths in many aspects of life, including finance. One of his famous quotes is: “Compound interest is the eighth wonder of the world. He who understands it, earns it; he who doesn’t, pays it.” (Quotes guide 2024).
Why did Einstein call It the eighth wonder? The reason why it is so profound from the previous exercises.
- Exponential Growth: As opposed to linear growth, where increases are constant, exponential growth means that the increases get larger with each period. This is why small regular investments can grow significantly over time.
- Time’s Power: The longer the period, the more powerful the effect. Even modest investments can grow to considerable amounts given enough time due to the compounding effect.
- Financial Wisdom: Understanding and utilizing compound interest is a characteristic of financial literacy. Those who grasp its power can use it to their advantage and investing wisely.
Summary
Teaching compound interest is about showing how interest can grow on itself over time, exponentially increasing the total amount. Using practical examples, like savings accounts or loans, makes the concept relatable. Visual aids, such as graphs and charts, can highlight how compound interest works over different periods. Emphasizing real-life applications helps students understand its importance.


